
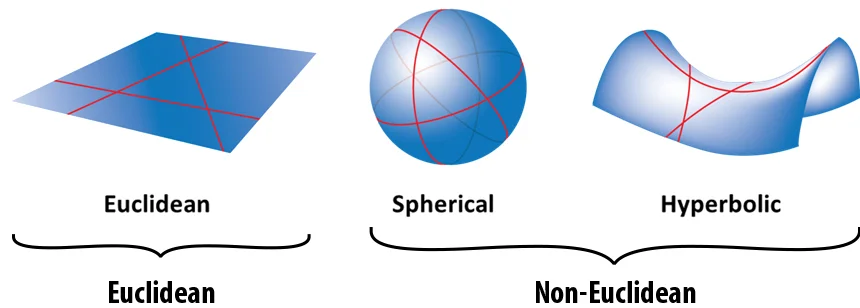
The present (sixth) edition clarifies some obscurities in the fifth, and includes a new section 15.9 on the author's useful concept of inversive distance. Euclidean and non-Euclidean geometry, and then it addresses the specific differences that constitute elliptic and hyperbolic geometry.

This treatment can be enjoyed by anyone who is familiar with algebra up to the elements of group theory. The word geometry is derived from the Greek words ‘geo’ meaning Earth and ‘metrein’ meaning ‘To measure’. Euclidean geometry is based on different axioms and theorems. He defined a basic set of rules and theorems for a proper study of geometry through his axioms and postulates. Euclids geometry is also called Euclidean Geometry. It is the study of planes and solid figures on the basis of axioms and postulates invited by Euclid. The area of a triangle is related to the sum of its angles by means of an ingenious idea of Gauss. Euclidean geometry is the study of 2-Dimensional geometrical shapes and figures. Euclids geometry is a type of geometry started by Greek mathematician Euclid. Elliptic and hyperbolic geometries are derived from real projective geometry by specializing in elliptic or hyperbolic polarity which transforms points into lines (in two dimensions), planes (in three dimensions), and vice versa.Īn unusual feature of the book is its use of the general linear transformation of coordinates to derive the formulas of elliptic and hyperbolic trigonometry. They lead in a natural way to isometries or 'congruent transformations.' Following a recommendation by Bertrand Russell, continuity is described in terms of order. Transformations that preserve incidence are called collineations. Before we discuss the material generally known as non Euclidean geometry, it will be helpful to summarize a few basic results from spherical geometry. This synthetic development is followed by the introduction of homogeneous coordinates, beginning with Von Staudt's idea of regarding points as entities that can be added or multiplied. Spherical geometry can be said to be the first non Euclidean geometry. Those numbered 834-866 are open to undergraduate students who have completed 45 semester hours of credit and to graduate students undergraduates are awarded upper division credit graduate students are awarded graduate credit.Throughout most of this book, non-Euclidean geometries in spaces of two or three dimensions are treated as specializations of real projective geometry in terms of a simple set of axioms concerning points, lines, planes, incidence, order and continuity, with no mention of the measurement of distances or angles. In two articles published in 18, Eugenio Beltrami, at the time professor at the University of Bologna, produced various models of the hyperbolic version non-Euclidean geometry, the one thought in solitude by Gauss, but developed and written by Lobachevsky and Bolyai. Workshops numbered 800-833 are open to all undergraduate and graduate students and are awarded lower division credit. 600-level courses are open to graduate students only.

There exist three non-collinear points in the plane. Given two points, there is one and only one line containing those points. In what is known as the Geometry of Compass, a straight line is defined by any pair of two. This item is available to borrow from 1 library branch.
Wolfe represents a specific, individual, material embodiment of a distinct intellectual or artistic creation found in University of Missouri-St. To earn graduate credit additional course requirements must be met. Absolute Geometry 1.1 The axioms 1.1.1 Properties of incidence Lines and points are primary notions, they are not dened. Well, this is what happens when you hang around Euclid for. The item Introduction to non-Euclidean geometry, by Harold E. Due to the controversy surrounding Euclid’s fifth postulate, other non-Euclidean geometries have evolved. 500-level classes are advanced undergraduate classes. supplementing the basic Euclidean geometry curriculum, as it is currently taught in high schools, with spherical geometry, a non-Euclidean geometry curriculum. Courses numbered 300-599 are designated as senior college (upper division) courses if completed at a regionally accredited four-year institution. Euclids text Elements was the first systematic discussion of geometry. Courses numbered 100-299 are designated as junior college (lower division) courses. Euclidean geometry is a mathematical well-known system attributed to the Greek mathematician Euclid of Alexandria. Courses numbered 000-099 are classified as developmental courses (unless a lab section which corresponds with a 100-599 lecture course).


 0 kommentar(er)
0 kommentar(er)
